Optimisation#
With the small tracking simulation time, Manzoni is well adapted
to perform optimisation of beamlines. An external Python library pymoo
is used to define optimization algorithm.
After defining a Manzoni input, the user must create a class for the optimisation. This class is over the form:
class Optimise_beamline(ElementwiseProblem):
def __init__(self, **kwargs):
super().__init__(
n_var=1,
n_obj=1,
n_ieq_constr=1,
xl=np.array([xa]),
xu=np.array([xb]),
**kwargs
)
def _evaluate(self, x, out, *args, **kwargs):
# mi is the Manzoni input line
mi.set_parameters("Element_name", {"parameter_name": value})
# compute the F and/or the G values
out["F"] = f_value
out["G"] = [g_values]
The entire list of algorithm is described at the following link: https://pymoo.org/algorithms/list.html
Warning
To perform Twiss matching, the user should use the method manzoni.twiss() as it is quicker and more precise than using a TwissObserver().
As example, let’s define a simple cell with three quadrupoles and two slits and we would like to have an asymmetry lower than 10% while keeping the transmission high.
import numpy as np
import georges
from georges.manzoni import Input
from georges.manzoni.beam import MadXBeam
from georges.manzoni import observers
from georges import vis
from pymoo.core.problem import ElementwiseProblem
from pymoo.termination import get_termination
from pymoo.algorithms.soo.nonconvex.pso import PSO
from pymoo.optimize import minimize
_ureg = georges.ureg
d1 = georges.Element.Drift(NAME="D1", L=0.2 * _ureg.m, APERTYPE="RECTANGULAR", APERTURE=[10 * _ureg.cm, 10 * _ureg.cm])
q1 = georges.Element.Quadrupole(
NAME="Q1", L=0.3 * _ureg.m, K1=-1 * _ureg.m**-2, APERTYPE="RECTANGULAR", APERTURE=[10 * _ureg.cm, 5 * _ureg.cm]
)
d2 = georges.Element.Drift(NAME="D2", L=0.2 * _ureg.m, APERTYPE="CIRCULAR", APERTURE=[10 * _ureg.cm, 10 * _ureg.cm])
sl1 = georges.Element.RectangularCollimator(
NAME="SL1", L=0.2 * _ureg.m, APERTYPE="RECTANGULAR", APERTURE=[0.0275 * _ureg.m, 0.0275 * _ureg.m]
)
d3 = georges.Element.Drift(NAME="D3", L=0.2 * _ureg.m, APERTYPE="CIRCULAR", APERTURE=[10 * _ureg.cm, 10 * _ureg.cm])
q2 = georges.Element.Quadrupole(
NAME="Q2", L=0.3 * _ureg.m, K1=5 * _ureg.m**-2, APERTYPE="RECTANGULAR", APERTURE=[10 * _ureg.cm, 5 * _ureg.cm]
)
d4 = georges.Element.Drift(NAME="D4", L=0.2 * _ureg.m, APERTYPE="CIRCULAR", APERTURE=[10 * _ureg.cm, 10 * _ureg.cm])
sl2 = georges.Element.RectangularCollimator(
NAME="SL2", L=0.2 * _ureg.m, APERTYPE="RECTANGULAR", APERTURE=[0.0275 * _ureg.m, 0.0275 * _ureg.m]
)
d5 = georges.Element.Drift(NAME="D5", L=0.2 * _ureg.m, APERTYPE="CIRCULAR", APERTURE=[10 * _ureg.cm, 10 * _ureg.cm])
q3 = georges.Element.Quadrupole(
NAME="Q3", L=0.3 * _ureg.m, K1=-4 * _ureg.m**-2, APERTYPE="RECTANGULAR", APERTURE=[10 * _ureg.cm, 5 * _ureg.cm]
)
d6 = georges.Element.Drift(NAME="D6", L=0.2 * _ureg.m, APERTYPE="CIRCULAR", APERTURE=[10 * _ureg.cm, 10 * _ureg.cm])
sequence = georges.PlacementSequence(name="Sequence")
sequence.place(d1, at_entry=0 * _ureg.m)
sequence.place_after_last(q1)
sequence.place_after_last(d2)
sequence.place_after_last(sl1)
sequence.place_after_last(d3)
sequence.place_after_last(q2)
sequence.place_after_last(d4)
sequence.place_after_last(sl2)
sequence.place_after_last(d5)
sequence.place_after_last(q3)
sequence.place_after_last(d6)
kin = georges.Kinematics(230 * _ureg.MeV, particle=georges.particles.Proton, kinetic=True)
sequence.metadata.kinematics = kin
beam = MadXBeam(
kinematics=kin,
distribution=georges.Distribution.from_5d_multigaussian_distribution(
n=1e3, xrms=0.01 * _ureg.cm, pxrms=0.01, yrms=0.05 * _ureg.cm, pyrms=0.005
).distribution.values,
)
mi = Input.from_sequence(sequence=sequence)
mi.freeze()
losses_observer = mi.track(beam=beam, observers=observers.LossesObserver())
symmetry_observer = mi.track(beam=beam, observers=observers.SymmetryObserver())
print(
f"""
Before optimisation
------------------
Transmission: {100 * (losses_observer.to_df().iloc[-1]['PARTICLES_OUT'] / losses_observer.to_df().iloc[0]['PARTICLES_IN'])}%
Asymmetry of the beam: {100*symmetry_observer.to_df().iloc[-1]['SYM_OUT']}%
"""
)
Before optimisation
------------------
Transmission: 95.0%
Asymmetry of the beam: 37.54982683238548%
manzoni_plot = vis.ManzoniMatplotlibArtist()
manzoni_plot.plot_cartouche(sequence.df)
manzoni_plot.losses(losses_observer)
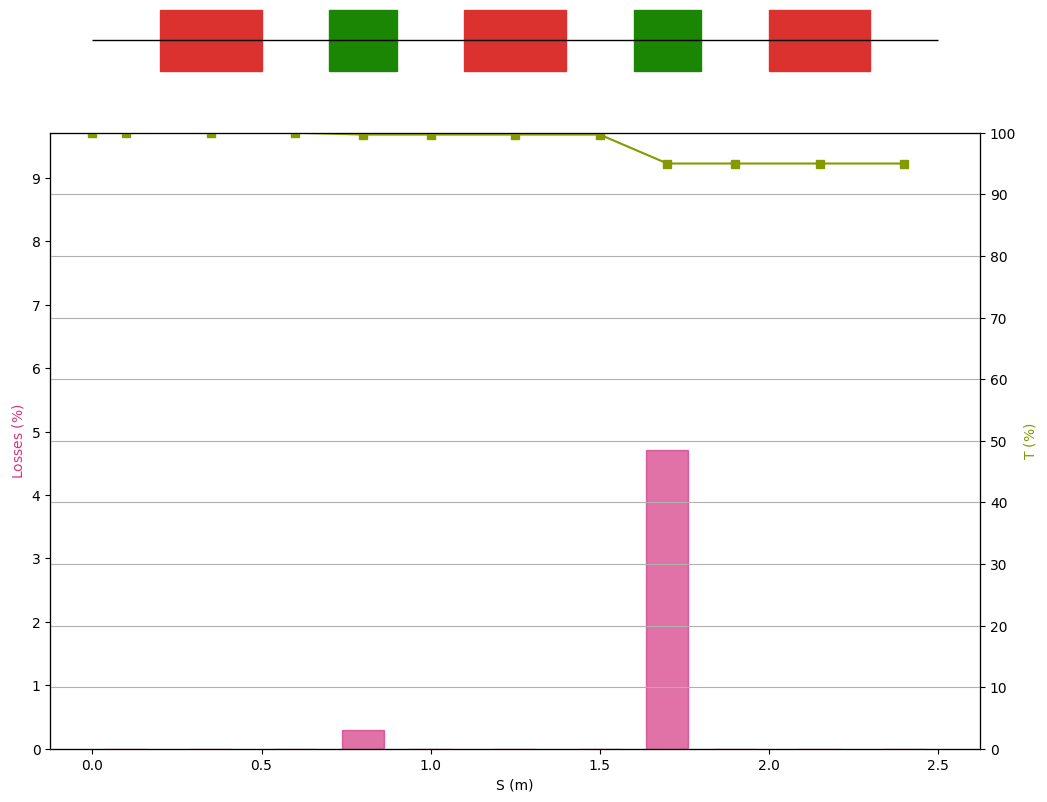
manzoni_plot = vis.ManzoniMatplotlibArtist()
manzoni_plot.plot_cartouche(sequence.df)
manzoni_plot.symmetry(symmetry_observer)
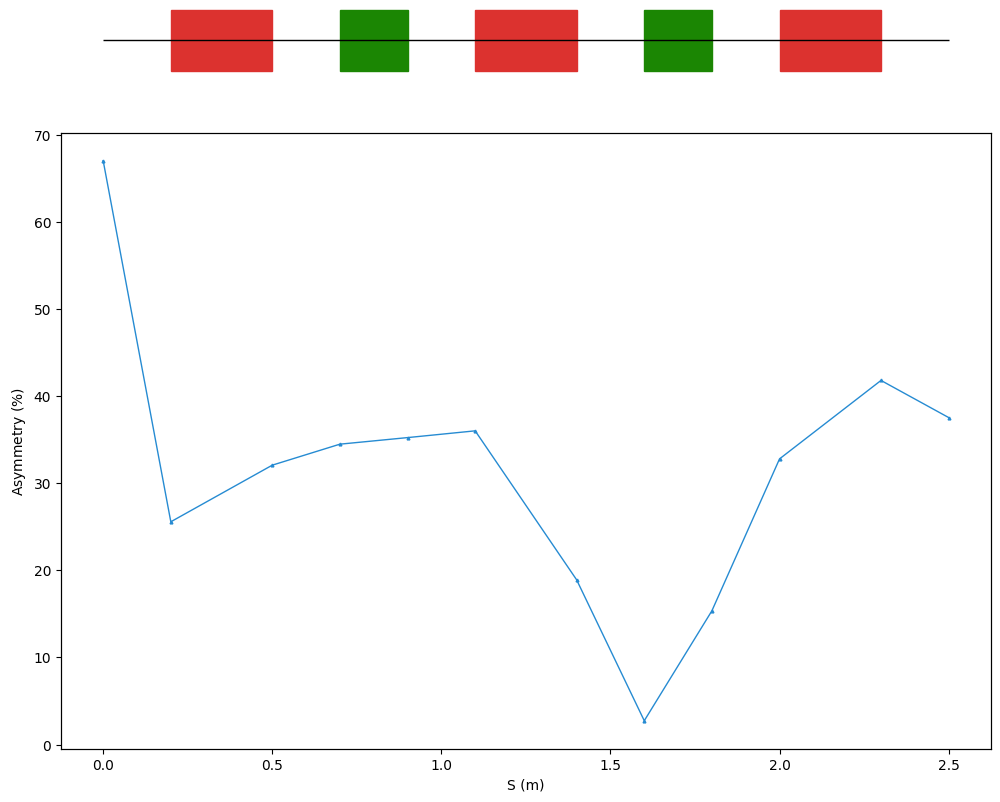
class Optimise_beamline(ElementwiseProblem):
def __init__(self, **kwargs):
super().__init__(
n_var=5,
n_obj=1,
n_ieq_constr=1,
xl=np.array([-10, 0, -10, 0.01, 0.01]),
xu=np.array([0, 10, 0, 0.0275, 0.0275]),
**kwargs
)
def _evaluate(self, x, out, *args, **kwargs):
mi.set_parameters("Q1", {"K1": x[0] * _ureg.m**-2})
mi.set_parameters("Q2", {"K1": x[1] * _ureg.m**-2})
mi.set_parameters("Q3", {"K1": x[2] * _ureg.m**-2})
mi.set_parameters("SL1", {"APERTURE": [x[3] * _ureg.m, 0.0275 * _ureg.m]})
mi.set_parameters("SL2", {"APERTURE": [0.0275 * _ureg.m, x[4] * _ureg.m]})
losses_observer = mi.track(beam=beam, observers=observers.LossesObserver(elements=["D6"]))
symmetry_observer = mi.track(beam=beam, observers=observers.SymmetryObserver(elements=["D6"]))
transmission = 100 * (
losses_observer.to_df().iloc[-1]["PARTICLES_OUT"] / losses_observer.to_df().iloc[0]["PARTICLES_IN"]
)
out["F"] = 1 / transmission
out["G"] = [100 * symmetry_observer.to_df().iloc[-1]["SYM_OUT"] - 10]
algorithm = PSO(pop_size=50)
problem = Optimise_beamline()
termination = get_termination("n_eval", 15000)
res = minimize(problem, algorithm, termination=termination, seed=1, verbose=False)
print("Best solution found: \nX = %s\nF = %s\nG = %s" % (res.X, res.F, res.G))
mi.set_parameters("Q1", {"K1": res.X[0] * _ureg.m**-2})
mi.set_parameters("Q2", {"K1": res.X[1] * _ureg.m**-2})
mi.set_parameters("Q3", {"K1": res.X[2] * _ureg.m**-2})
mi.set_parameters("SL1", {"APERTURE": [res.X[3] * _ureg.m, 0.0275 * _ureg.m]})
mi.set_parameters("SL2", {"APERTURE": [0.0275 * _ureg.m, res.X[4] * _ureg.m]})
losses_observer = mi.track(beam=beam, observers=observers.LossesObserver())
symmetry_observer = mi.track(beam=beam, observers=observers.SymmetryObserver())
Best solution found:
X = [-3.40267848 9.74125756 -4.23449477 0.01521261 0.01801969]
F = [0.01]
G = [-2.33348197]
print(
f"""
After optimisation
------------------
Transmission: {100 * (losses_observer.to_df().iloc[-1]['PARTICLES_OUT'] / losses_observer.to_df().iloc[0]['PARTICLES_IN'])}%
Asymmetry of the beam: {100*symmetry_observer.to_df().iloc[-1]['SYM_OUT']}%
"""
)
After optimisation
------------------
Transmission: 61.9%
Asymmetry of the beam: 7.66651802756707%
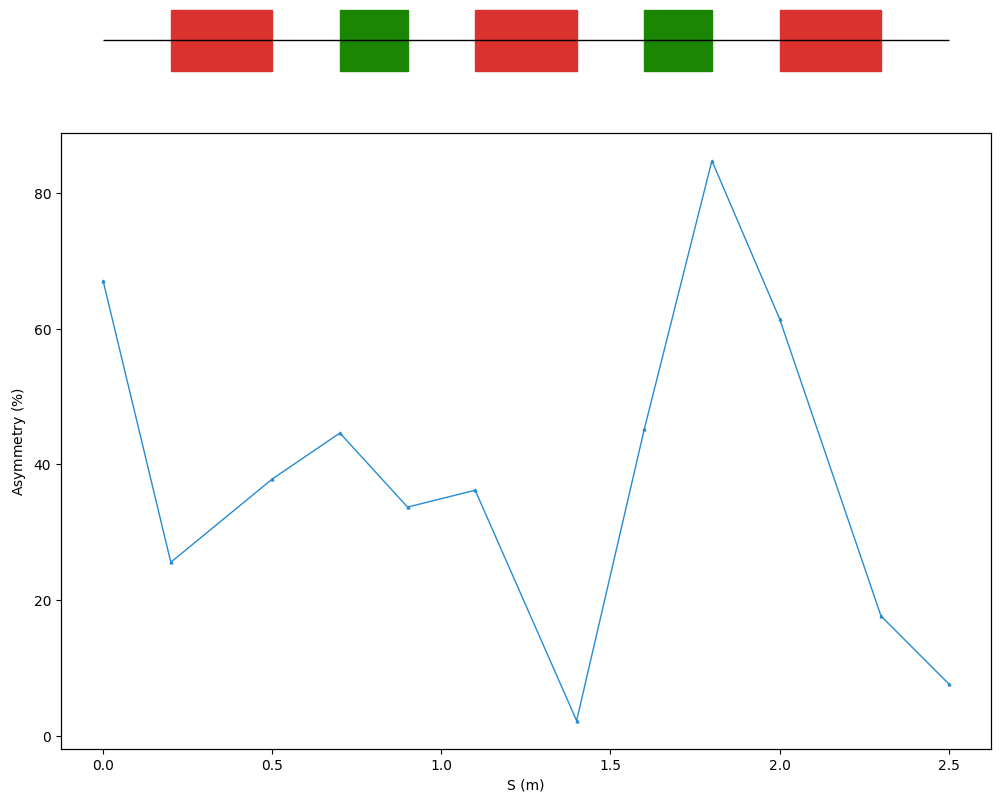
manzoni_plot = vis.ManzoniMatplotlibArtist()
manzoni_plot.plot_cartouche(sequence.df)
manzoni_plot.losses(losses_observer)
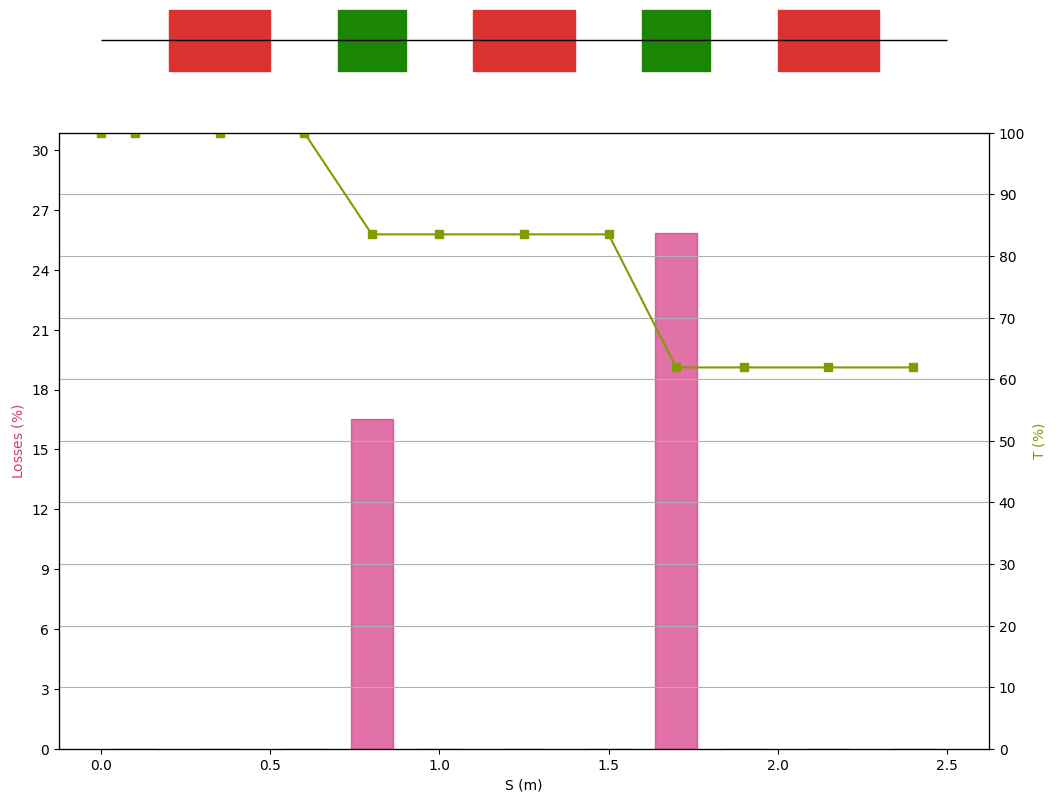
manzoni_plot = vis.ManzoniMatplotlibArtist()
manzoni_plot.plot_cartouche(sequence.df)
manzoni_plot.symmetry(symmetry_observer)