Particle tracking with energy degradation#
We replace the collimator from the previous example by an 10cm length energy degrader in Beryllium. The parameters WITH_LOSSES can be set to True` or False` depending the application. If it is set to True, the particles are randomly lost. The number of lost particles depends on the material and the kinetic energy and the coefficient are computed as described in the Fermi module.
c1 = georges.Element.Degrader(NAME='DEG',
MATERIAL=georges.fermi.materials.Beryllium,
L = 10*_ureg.cm,
WITH_LOSSES=True
)
Let’s first import the necessary packages
import matplotlib.pyplot as plt
import georges
from georges import ureg as _ureg
from georges import vis
from georges.manzoni import Input, observers
from georges.manzoni.beam import MadXBeam
Let’s define the line using a PlacementSequence#
d1 = georges.Element.Drift(
NAME="D1",
L=0.3 * _ureg.m,
APERTYPE="RECTANGULAR",
APERTURE=[5 * _ureg.cm, 3 * _ureg.cm],
)
qf = georges.Element.Quadrupole(
NAME="Q1",
L=0.3 * _ureg.m,
K1=2 * _ureg.m**-2,
APERTYPE="RECTANGULAR",
APERTURE=[5 * _ureg.cm, 3 * _ureg.cm],
)
d2 = georges.Element.Drift(
NAME="D2",
L=0.3 * _ureg.m,
APERTYPE="CIRCULAR",
APERTURE=[5 * _ureg.cm, 5 * _ureg.cm],
)
b1 = georges.Element.SBend(
NAME="B1",
L=1 * _ureg.m,
ANGLE=30 * _ureg.degrees,
K1=0 * _ureg.m**-2,
APERTYPE="CIRCULAR",
APERTURE=[5 * _ureg.cm, 5 * _ureg.cm],
)
d3 = georges.Element.Drift(
NAME="D3",
L=0.3 * _ureg.m,
APERTYPE="CIRCULAR",
APERTURE=[5 * _ureg.cm, 5 * _ureg.cm],
)
qd = georges.Element.Quadrupole(
NAME="Q2",
L=0.3 * _ureg.m,
K1=-2 * _ureg.m**-2,
APERTYPE="RECTANGULAR",
APERTURE=[5 * _ureg.cm, 3 * _ureg.cm],
)
d4 = georges.Element.Drift(
NAME="D4",
L=0.3 * _ureg.m,
APERTYPE="CIRCULAR",
APERTURE=[5 * _ureg.cm, 5 * _ureg.cm],
)
c1 = georges.Element.Degrader(NAME='DEG',
MATERIAL=georges.fermi.materials.Beryllium,
L = 10*_ureg.cm,
WITH_LOSSES=True
)
d5 = georges.Element.Drift(
NAME="D5",
L=0.3 * _ureg.m,
APERTYPE="CIRCULAR",
APERTURE=[5 * _ureg.cm, 5 * _ureg.cm],
)
b2 = georges.Element.SBend(
NAME="B2",
L=1 * _ureg.m,
ANGLE=-30 * _ureg.degrees,
K1=0 * _ureg.m**-2,
APERTYPE="RECTANGULAR",
APERTURE=[5 * _ureg.cm, 3 * _ureg.cm],
)
d6 = georges.Element.Drift(
NAME="D6",
L=0.3 * _ureg.m,
APERTYPE="CIRCULAR",
APERTURE=[5 * _ureg.cm, 5 * _ureg.cm],
)
sequence = georges.PlacementSequence(name="Sequence")
sequence.place(d1, at_entry=0 * _ureg.m)
sequence.place_after_last(qf)
sequence.place_after_last(d2)
sequence.place_after_last(b1)
sequence.place_after_last(d3)
sequence.place_after_last(c1)
sequence.place_after_last(d4)
sequence.place_after_last(qd)
sequence.place_after_last(d5)
sequence.place_after_last(b2)
sequence.place_after_last(d6)
We use a Gaussian beam with an energy of 230 MeV#
kin = georges.Kinematics(230 * _ureg.MeV, particle=georges.particles.Proton, kinetic=True)
sequence.metadata.kinematics = kin
beam = MadXBeam(
kinematics=kin,
distribution=georges.Distribution.from_5d_multigaussian_distribution(
n=10000, xrms=0.1 * _ureg.cm, yrms=0.7 * _ureg.cm, pxrms=0.01, pyrms=0.01
).distribution.values,
)
We can now track in our line with Manzoni#
mi = Input.from_sequence(sequence=sequence)
We need to adjust the energy of the line in presence of an energy degrader.
mi.adjust_energy(input_energy=kin.ekin)
Let’s freeze the sequence and run Manzoni
mi.freeze()
beam_observer_std = mi.track(beam=beam, observers=observers.SigmaObserver())
beam_observer_beam = mi.track(beam=beam, observers=observers.BeamObserver(with_input_beams=True))
beam_observer_losses = mi.track(beam=beam, observers=observers.LossesObserver())
Plot results#
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
manzoni_plot = vis.ManzoniMatplotlibArtist(ax=ax)
manzoni_plot.plot_cartouche(sequence.df)
manzoni_plot.tracking(beam_observer_std, plane="both")
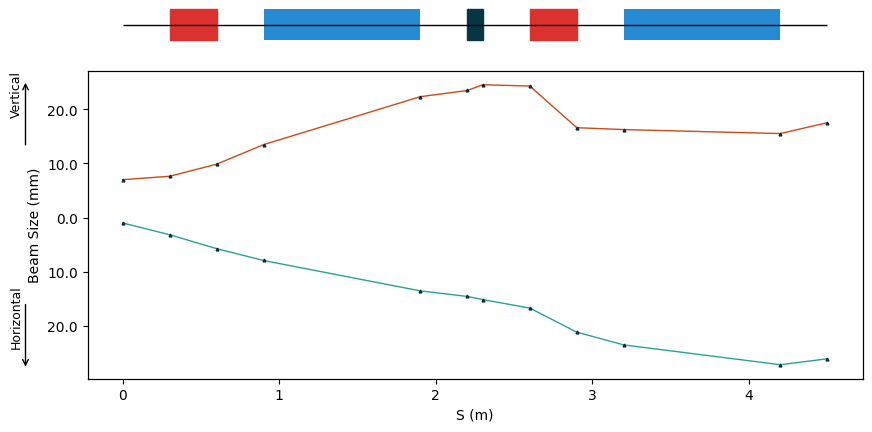
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
manzoni_plot = vis.ManzoniMatplotlibArtist(ax=ax)
manzoni_plot.plot_cartouche(sequence.df)
manzoni_plot.losses(beam_observer_losses, log_scale=False)
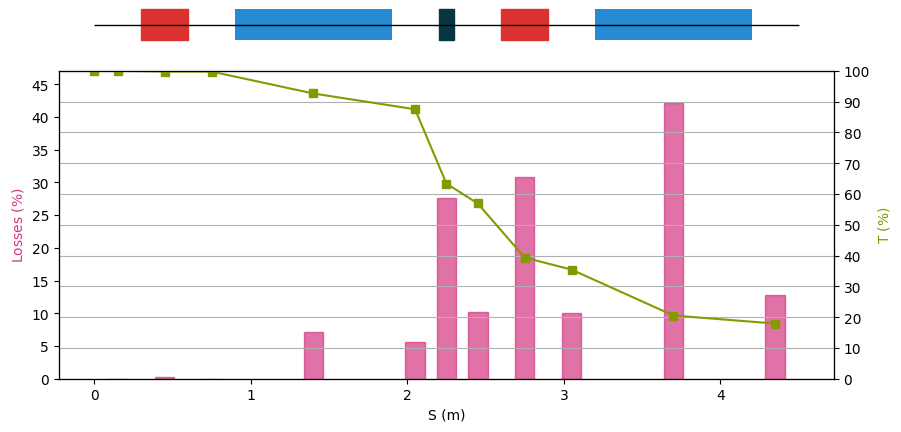
fig = plt.figure(figsize=(10,4))
ax = fig.add_subplot(111)
manzoni_plot = vis.ManzoniMatplotlibArtist(ax=ax)
manzoni_plot.plot_cartouche(sequence.df)
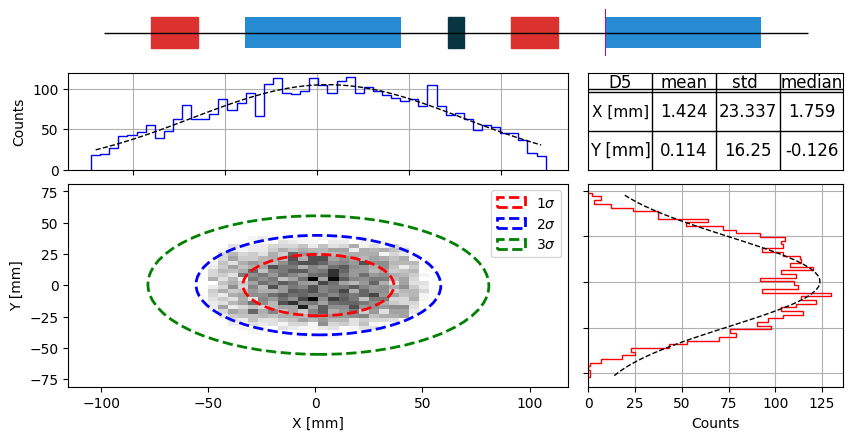
manzoni_plot.phase_space(beam_observer_beam, element="D5")