Observers

Different observers are implemented in Manzoni. The syntax is as follow

observer = Observer(element=['eleA', 'eleB'])

The results are stored in a pandas.DataFrame and are available using:

result = observer.to_df()

In the sections below, we detail each observer implemented in Manzoni

MeanObserver

This observer store the mean of each quantity in the beam (\(\bar{x}\), \(\bar{px}\), \(\bar{y}\), \(\bar{py}\), \(\bar{dpp}\))

observer = MeanObserver(element=['eleA', 'eleB'])

StdObserver

This observer store the standard deviation of each quantity in the beam (\(\sigma_x\), \(\sigma_{px}\), \(\sigma_y\), \(\sigma_{p}y\), \(\sigma_{dpp}\))

observer = StdObserver(element=['eleA', 'eleB'])

BeamObserver

This observer store the entire beam distribution at the exit of an element. If the flag input with_input_beams is set to True, the beam at the entrance of the element is also stored.

observer = BeamObserver(element=['eleA', 'eleB'], with_input_beams=True)

LossesObserver

This observer store the number of particles, the losses and the transmission of an element.

observer = LossesObserver(element=['eleA', 'eleB'])

SymmetryObserver

This observer compute the symmetry of the beam at the entrance and at the exit of an element. The symmetry is given by the following relation:

\[sym = \left| \frac{(\sigma_x - \sigma_y)}{(\sigma_x + \sigma_y)} \right|\]

observer = SymmetryObserver(element=['eleA', 'eleB'])

IbaBPMObserver

This observer is used to validate the model with the IBA’ Beam Profile Monitor. A Gaussian fit is performed directly on the beam position data. The element to store the data must be a Marker.

observer = IbaBpmObserver(element=['eleA', 'eleB'])

UserObserver

It is also possible to define his own observer. First, you must create a class that inherits from the main Observer. The method __call__(self, element, b1, b2) receives the element where to store data and the beam at the entry and exit of an element. The example below illustrates the implementation of a mean observer.

class MyMeanObserver(georges.manzoni.Observer):
    def __init__(self, elements = None):
        super().__init__(elements)
        self.headers = ('NAME',
                        'AT_ENTRY',
                        'AT_CENTER',
                        'AT_EXIT',
                        'BEAM_IN_X',
                        'BEAM_OUT_X',
                        'BEAM_IN_Y',
                        'BEAM_OUT_Y',
                        'BEAM_IN_XP',
                        'BEAM_OUT_XP',
                        'BEAM_IN_YP',
                        'BEAM_OUT_YP',
                        'BEAM_IN_DPP',
                        'BEAM_OUT_DPP',
                        )

    def __call__(self, element, b1, b2):
        if super().__call__(element, b1, b2):
            self.data.append((element.NAME,
                              element.AT_ENTRY,
                              element.AT_CENTER,
                              element.AT_EXIT,
                              b1[:, 0].mean(),
                              b2[:, 0].mean(),
                              b1[:, 2].mean(),
                              b2[:, 2].mean(),
                              b1[:, 1].mean(),
                              b2[:, 1].mean(),
                              b1[:, 3].mean(),
                              b2[:, 3].mean(),
                              b1[:, 4].mean(),
                              b2[:, 4].mean(),
                              ))

Now this observer can be used by Manzoni:

beam_Myobserver = mi.track(beam=beam, observers=MyMeanObserver())

Classes

BeamObserver([elements, with_input_beams])	Return the beam distribution at the exit of an element.
Distribution([distribution])	Particle beam to be tracked in a beamline or accelerator model.
IbaBpmObserver([elements])
LossesObserver([elements])	Compute the losses and the transmission in an element.
MeanObserver([elements])	Compute the mean values of the beam coordinates.
Model(func[, independent_vars, param_names, ...])	Create a model from a user-supplied model function.
Observer(elements)
ObserverType
Parameters([usersyms])	A dictionary of Parameter objects.
SigmaObserver([elements])	Compute the standard deviation of the beam coordinates.
SuperObserver([elements])
SymmetryObserver([elements])	Compute the symmetry of the beam.
TwissObserver([elements])	Compute the Twiss parameters of the beam.

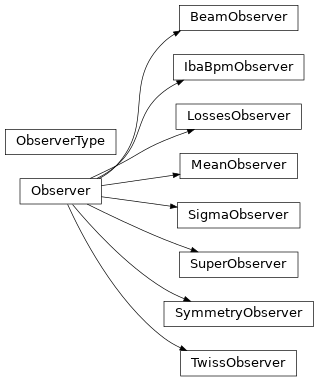
Class Inheritance Diagram